Structural Equation Models
Simply speaking, a structural equation model (SEM) is a combination of confirmatory factor analysis and path analysis. Structural equation modeling includes two sets of models – the measurement model and the structural model. The measurement model can be expressed as a factor model. Figure 1 is a model to measure cognitive ability using three variables – verbal ability, math ability, and speed ability (note each of them can be viewed as factors measured by lower level observed variables).
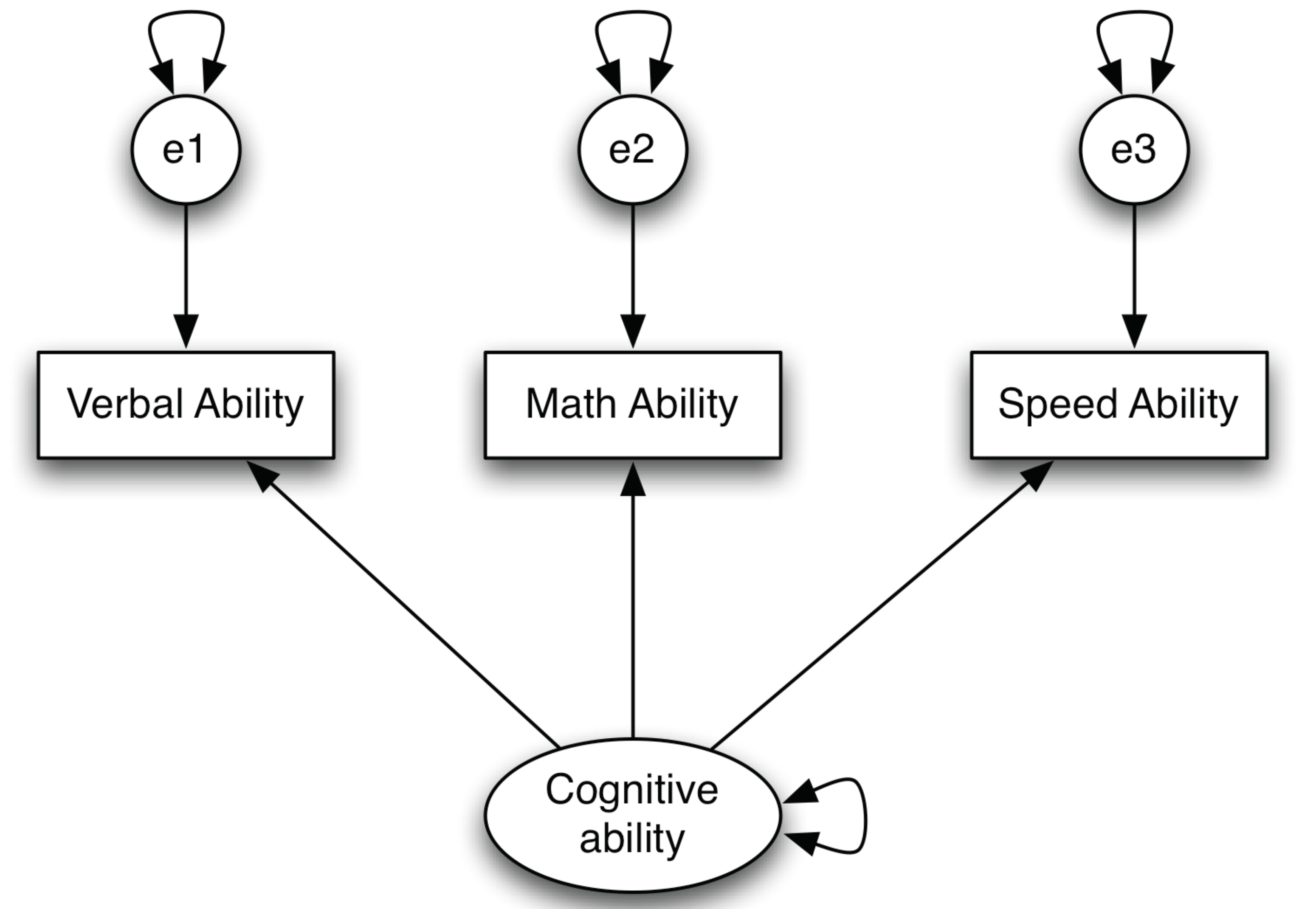
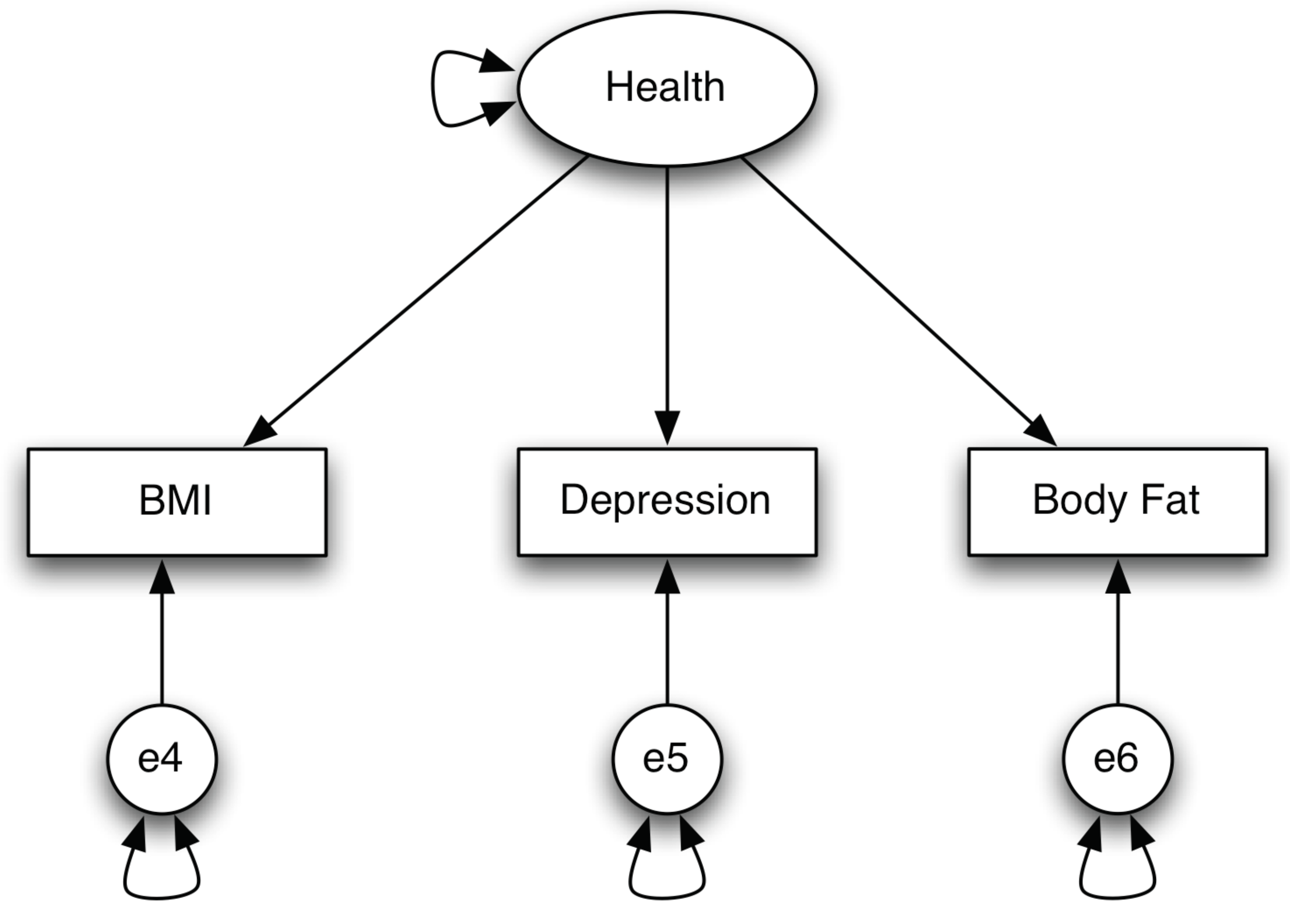
Figure 2 gives another example of measurement model – a model to measure health.
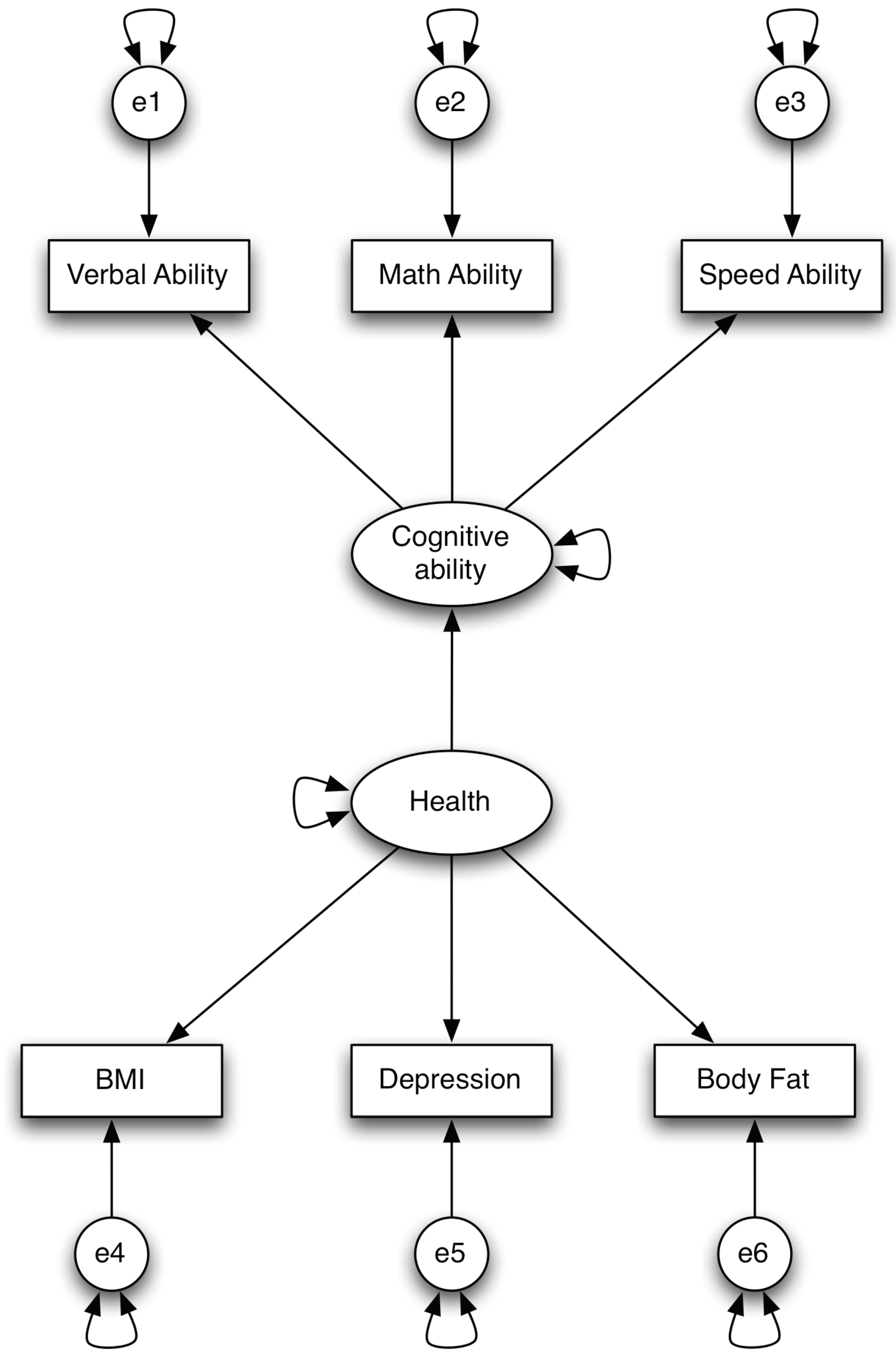
If one believes that health influences cognitive ability, then one can fit a path model using the factors – cognitive ability and health. Therefore, a structural model is actually a path model. Putting them together, we have a model in Figure 3. This model is called SEM model.
Example 1. Autoregressive model
In ACTIVE study, we have three variables – word series (ws), letter series (ls), and letter sets (ls) to measure reasoning ability. Also, we have data on all these three variables before and after training. Assume we want to test whether reasoning ability before training can predict reasoning ability after training. Then the SEM model in Figure 4 can be used. Not that we allow the factor in time 1 to predict the factor at time 2. In addition, we allow the uniqueness factors for each observed variable to be correlated. The R code for the analysis is given below.

First look at model fit. The chi-square value is 27 with 5 degrees of freedom. The p-value for chi-square test is almost 0. Thus, based on chi-square test, this is not a good model. However, CFI and TFI are both close to 1. The RMSEA is about 0.063 and SRMR is about 0.011. Considering the sample size here is large – N=1114, overall, we may accept this model is a fairly good model. Then we can answer our question. Because the regression coefficient from reasoning1 to reasoning2 is significant, reasoning ability before training seems to predict reasoning ability after training. In other words, those with higher reasoning ability before training tend to have higher reasoning ability after training.
> library(lavaan)
This is lavaan 0.5-23.1097
lavaan is BETA software! Please report any bugs.
> usedata('active.full.csv')
> automodel <- '
+ reasoning1 =~ ws1 + ls1 + lt1
+ reasoning2 =~ ws2 + ls2 + lt2
+ reasoning2 ~ reasoning1
+ ws1 ~~ ws2
+ ls1 ~~ ls2
+ lt1 ~~ lt2
+ '
>
> auto.res <- sem(automodel, data=active.full)
> summary(auto.res, fit=TRUE)
lavaan (0.5-23.1097) converged normally after 66 iterations
Number of observations 1114
Estimator ML
Minimum Function Test Statistic 27.213
Degrees of freedom 5
P-value (Chi-square) 0.000
Model test baseline model:
Minimum Function Test Statistic 5827.630
Degrees of freedom 15
P-value 0.000
User model versus baseline model:
Comparative Fit Index (CFI) 0.996
Tucker-Lewis Index (TLI) 0.989
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -16447.377
Loglikelihood unrestricted model (H1) -16433.771
Number of free parameters 16
Akaike (AIC) 32926.755
Bayesian (BIC) 33007.006
Sample-size adjusted Bayesian (BIC) 32956.186
Root Mean Square Error of Approximation:
RMSEA 0.063
90 Percent Confidence Interval 0.041 0.087
P-value RMSEA <= 0.05 0.151
Standardized Root Mean Square Residual:
SRMR 0.013
Parameter Estimates:
Information Expected
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|)
reasoning1 =~
ws1 1.000
ls1 1.192 0.030 40.091 0.000
lt1 0.422 0.016 26.301 0.000
reasoning2 =~
ws2 1.000
ls2 1.110 0.026 43.371 0.000
lt2 0.411 0.014 29.443 0.000
Regressions:
Estimate Std.Err z-value P(>|z|)
reasoning2 ~
reasoning1 1.073 0.024 43.919 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
.ws1 ~~
.ws2 1.216 0.327 3.718 0.000
.ls1 ~~
.ls2 0.356 0.401 0.888 0.375
.lt1 ~~
.lt2 1.596 0.138 11.544 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.ws1 5.511 0.385 14.324 0.000
.ls1 4.547 0.475 9.575 0.000
.lt1 3.996 0.181 22.065 0.000
.ws2 5.021 0.419 11.995 0.000
.ls2 5.161 0.507 10.182 0.000
.lt2 3.963 0.181 21.875 0.000
reasoning1 19.103 1.060 18.014 0.000
.reasoning2 2.447 0.289 8.479 0.000
>
Example 2. Mediation analysis with latent variables
In path analysis, we have fitted a complex mediation model. Since we know that ws1, ls1, and lt1 are measurements of reasoning ability, we can form a latent reasoning ability variable. Thus, our mediation model can be expressed as in Figure 5.

Given CFI = 0.997, RMSEA = 0.034 and SRMR = 0.015, we accept the model as a good model even though the chi-square test is significant. Based on the Sobel test, the total indirect effect from age to ept1 through hvltt1 and reasoning is significant.
> library(lavaan)
This is lavaan 0.5-23.1097
lavaan is BETA software! Please report any bugs.
> usedata('active.full.csv')
> #head(active.full)
> med.model <- '
+ reasoning =~ ws1 + ls1 + lt1
+ reasoning ~ p4*age + p8*edu
+ hvltt1 ~ p2*age + p7*edu
+ hvltt1 ~~ reasoning
+ ept1 ~ p1*age + p6*edu + p3*hvltt1 + p5*reasoning
+ indirect := p2*p3 + p4*p5
+ total := p1 + p2*p3 + p7*p3
+ '
>
> med.res <- sem(med.model, data=active.full)
> summary(med.res, fit=TRUE)
lavaan (0.5-23.1097) converged normally after 51 iterations
Number of observations 1114
Estimator ML
Minimum Function Test Statistic 18.363
Degrees of freedom 8
P-value (Chi-square) 0.019
Model test baseline model:
Minimum Function Test Statistic 3344.605
Degrees of freedom 20
P-value 0.000
User model versus baseline model:
Comparative Fit Index (CFI) 0.997
Tucker-Lewis Index (TLI) 0.992
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -20675.968
Loglikelihood unrestricted model (H1) -20666.787
Number of free parameters 17
Akaike (AIC) 41385.937
Bayesian (BIC) 41471.204
Sample-size adjusted Bayesian (BIC) 41417.207
Root Mean Square Error of Approximation:
RMSEA 0.034
90 Percent Confidence Interval 0.013 0.055
P-value RMSEA <= 0.05 0.889
Standardized Root Mean Square Residual:
SRMR 0.015
Parameter Estimates:
Information Expected
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|)
reasoning =~
ws1 1.000
ls1 1.181 0.029 41.262 0.000
lt1 0.430 0.016 26.758 0.000
Regressions:
Estimate Std.Err z-value P(>|z|)
reasoning ~
age (p4) -0.228 0.023 -9.737 0.000
edu (p8) 0.745 0.047 15.792 0.000
hvltt1 ~
age (p2) -0.161 0.027 -6.074 0.000
edu (p7) 0.429 0.052 8.177 0.000
ept1 ~
age (p1) 0.030 0.022 1.389 0.165
edu (p6) 0.396 0.046 8.527 0.000
hvltt1 (p3) 0.169 0.026 6.488 0.000
reasoning (p5) 0.643 0.035 18.186 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
.reasoning ~~
.hvltt1 7.255 0.592 12.263 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.ws1 5.334 0.366 14.594 0.000
.ls1 4.850 0.444 10.910 0.000
.lt1 3.917 0.181 21.657 0.000
.hvltt1 20.618 0.874 23.601 0.000
.ept1 11.505 0.522 22.027 0.000
.reasoning 13.814 0.777 17.777 0.000
Defined Parameters:
Estimate Std.Err z-value P(>|z|)
indirect -0.174 0.019 -9.368 0.000
total 0.075 0.025 3.008 0.003
>
To cite the book, use:
Zhang, Z. & Wang, L. (2017-2026). Advanced statistics using R. Granger, IN: ISDSA Press. https://doi.org/10.35566/advstats. ISBN: 978-1-946728-01-2.
To take the full advantage of the book such as running analysis within your web browser, please subscribe.
